Phasespace

This is an example of plotting phase space distributions. First, create a simple line, a tracker and a particle set:

Show imports

Hide code cell content

%load_ext autoreload
%autoreload 2

import xtrack as xt
import xpart as xp
import xplt
import numpy as np

np.random.seed(43543557)

xplt.apply_style()

Show line generation code

Hide code cell content

## Generate a simple 6-fold symmetric FODO lattice

n = 6  # number of sections
elements = {
    "QF": xt.Multipole(length=0.3, knl=[0, +0.63]),
    "QD": xt.Multipole(length=0.3, knl=[0, -0.48]),
    "MU": xt.Multipole(length=0.5, knl=[np.pi / n], hxl=[np.pi / n]),
}
parts = {
    "a": [
        xt.Node(0.7, "QF"),
        xt.Node(1.4, "MU"),
        xt.Node(2.1, "QD"),
        xt.Node(2.8, "MU"),
    ],
    "b": [
        xt.Node(2.2, "MU"),
        xt.Node(2.9, "QD"),
        xt.Node(3.6, "MU"),
        xt.Node(4.3, "QF"),
    ],
}
nodes = [xt.Node(5.0 * i, "a" if i % 2 else "b", name=f"S{i+1}") for i in range(n)]

line = xt.Line.from_sequence(
    nodes, length=5.0 * n, sequences=parts, elements=elements, auto_reorder=True
)
line = line.cycle(4)
line.particle_ref = xp.Particles()
line.build_tracker();

Show particle generation code

Hide code cell content

## Generate particles
nparticles = int(1e4)

# Transverse distribution (gaussian)
norm_emitt_x = 4e-6  # normalized 1-sigma emittance in m*rad (=beta*gamma*emitt_x)
norm_emitt_y = 1e-6  # normalized 1-sigma emittance in m*rad (=beta*gamma*emitt_y)
x, px = xp.generate_2D_gaussian(nparticles)
y, py = xp.generate_2D_gaussian(nparticles)

# Longitudinal distribution (coasting beam)
rel_momentum_spread = 1e-4  # relative momentum spread ( P/p0 - 1 )
zeta = line.get_length() * np.random.uniform(-0.5, 0.5, nparticles)
delta = rel_momentum_spread * xp.generate_2D_gaussian(nparticles)[0]

particles = line.build_particles(
    x_norm=x,
    px_norm=px,
    nemitt_x=norm_emitt_x,
    y_norm=y,
    py_norm=py,
    nemitt_y=norm_emitt_y,
    method="4d",  # for twiss (default is 6d, won't work without a cavity)
    zeta=zeta,
    delta=delta,
)

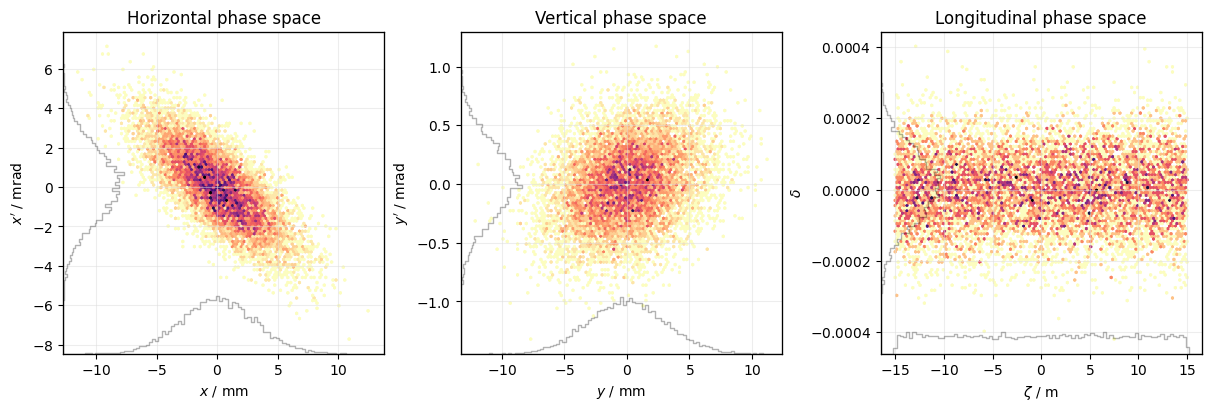
Default phasespace plot

Create a default PhasespacePlot:

plot = xplt.PhaseSpacePlot(particles)

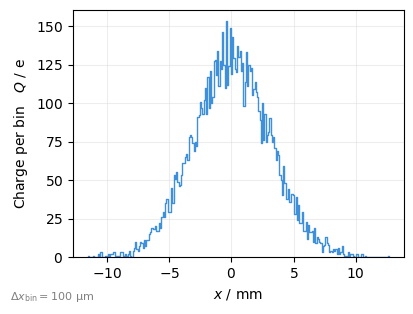
1D Histograms can also be plotted using ParticleHistogramPlot.
By default the particle count per bin is plotted, here we use kind= to plot the charge instead:

plot = xplt.ParticleHistogramPlot(
    "x", particles, kind="charge", bin_width=1e-4, figsize=(4, 3)
)  # bin_width is in data units (m)

Customisation

Use the parameter kind to specify what is plotted as a comma separated list of pairs a-b. The properties a and b can be any property of a particle such as x, px, y, delta, zeta, Jx, Θy etc. Note that zeta is the absolute value, while zeta_wrapped is the wrapped value in range (-circumference/2 ; +circumference/2). See Default properties for a complete list of default properties and refer to Adding custom data properties for an explanation of how to add custom ones.

Tip

The kind= parameter accepts abbreviations for common pairs, e.g. x for x-px, z for zeta-delta or Y for Y-Py

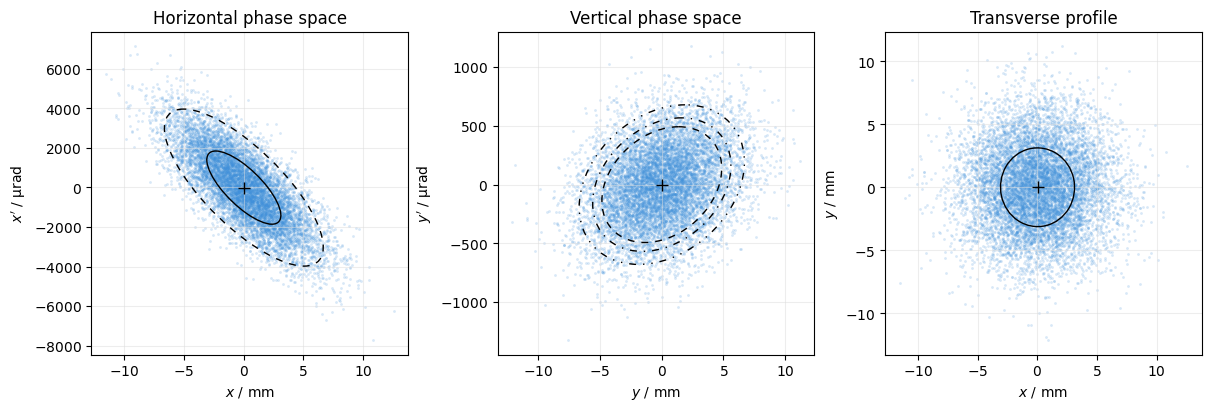
Here we also add some ellipses to indicate standard deviation and percentiles, disable the default projections, and use a scatter plot with some transparency. See PhasespacePlot for details.

plot = xplt.PhaseSpacePlot(
    particles,
    mask=particles.particle_id < 1e4,
    kind="x,y,x-y",
    plot="scatter",  # using a scatter plot instead of a 2D histogram
    scatter_kwargs=dict(alpha=0.2),  # scatter plot with semi-transparent color
    projections=False,  # No projections onto axes
    display_units=dict(p="urad"),  # p as shorthand for px and py
    mean=True,  # show mean cross for all
    std=[True, None, True],  # show std ellipse for first and last
    percentiles=[[90], [70, 80, 90], None],  # show some percentile ellipses
)
plot.ax[2].set(title="Transverse profile");

Tip

Most parameters accept a list of values to specify different values for each subplot

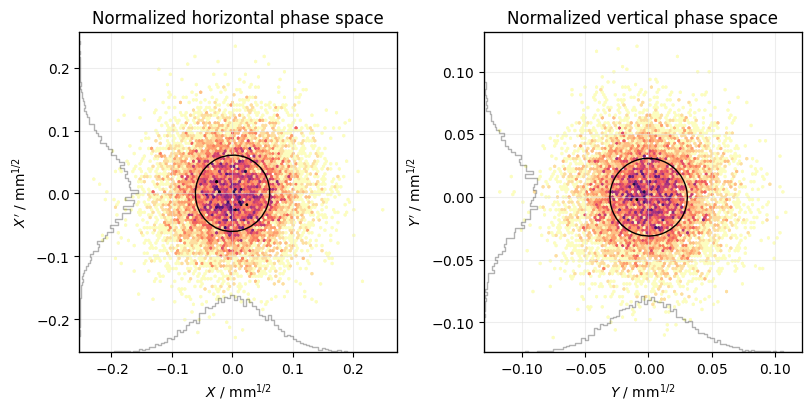
Normalized coordinates

Calculate twiss parameters for normalization:

tw = line.twiss(
    method="4d",
    at_elements=np.unique(particles.at_element),  # twiss at location of particles
)

Use uppercase letters for normalized coordinates (X is the shorthand for X-Px):

plot = xplt.PhaseSpacePlot(particles, kind="X,Y-Py", twiss=tw, std=True)

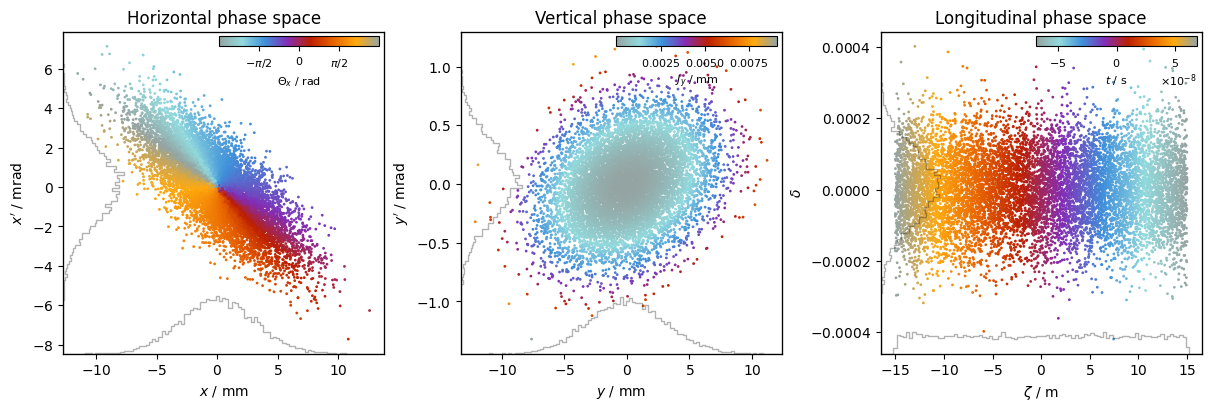
Color by 3rd coordinate

plot = xplt.PhaseSpacePlot(
    particles,
    "x,y,zeta_wrapped-delta",
    color="Θx,Jy,t",  # <-- color by value
    cmap="petroff_cyclic",
    cbar_loc="inside upper right",
    twiss=tw,
    grid=False,
)

Monitor data

Track the particle for a couple of turns:

line.track(particles, num_turns=100, turn_by_turn_monitor=True)

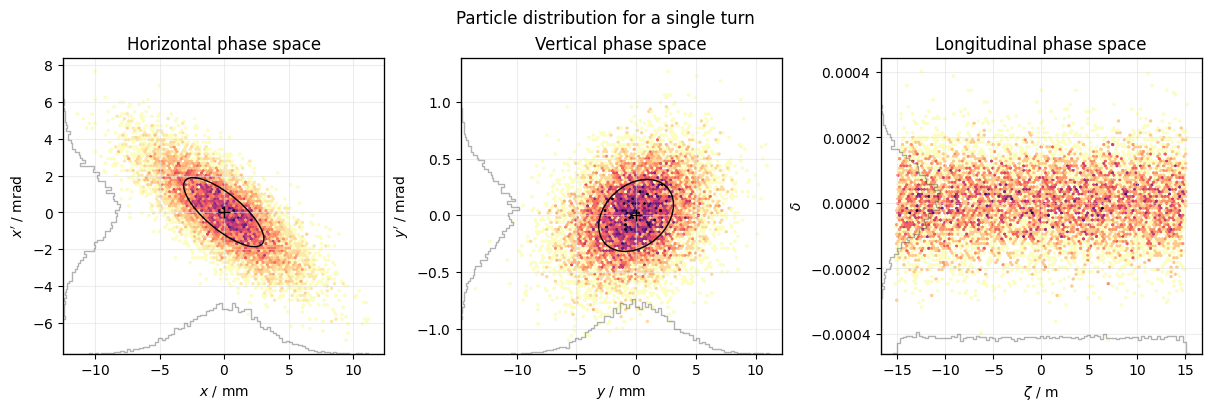
Use mask= to select a subset of the data to plot, e.g. a single turn:

plot = xplt.PhaseSpacePlot(
    line.record_last_track,
    mask=(slice(None), 83),  # select all particles and turn 83
    mean=(1, 1, 0),
    std=(1, 1, 0),
)
plot.fig.suptitle("Particle distribution for a single turn");

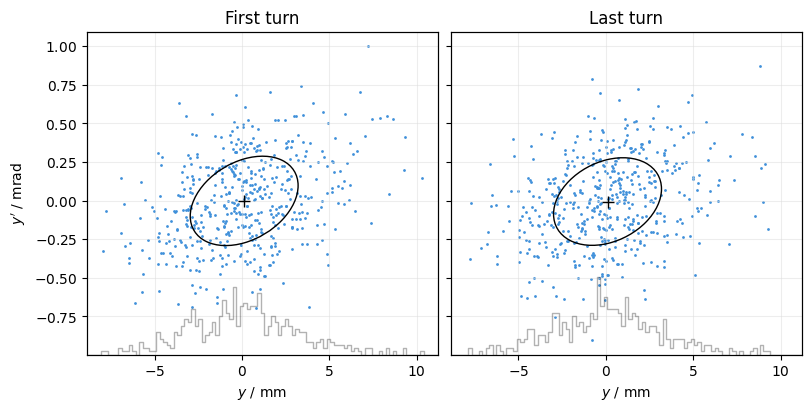
Use masks= to set a different mask for each subplot:

plot = xplt.PhaseSpacePlot(
    line.record_last_track,
    kind="y,y",
    titles=("First turn", "Last turn"),
    sharex="all",
    sharey="all",
    masks=[
        (slice(500), 0),
        (slice(500), -1),
    ],  # select 500 particles at first and last turn
    projections="x",
    mean=True,
    std=True,
)
plot.ax[1].set(ylabel=None);

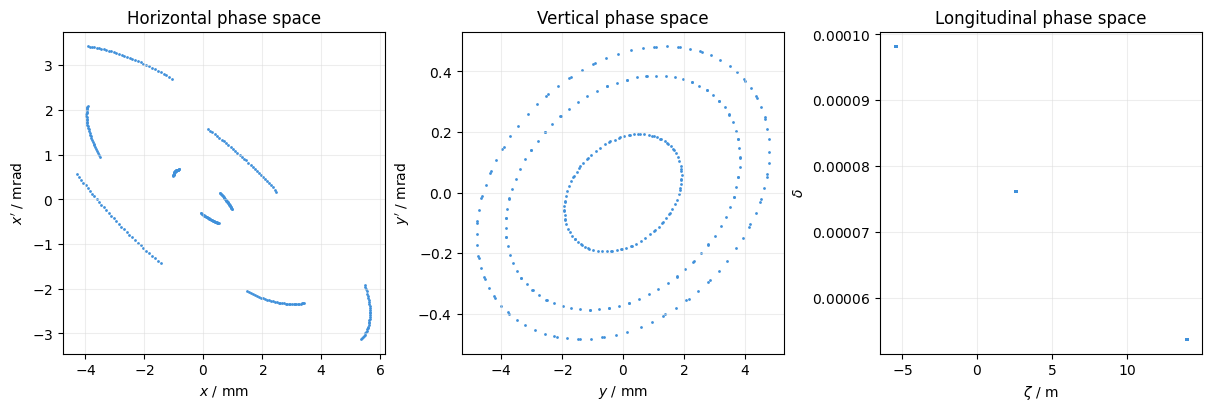
Plot the trace of some particles:

plot = xplt.PhaseSpacePlot(
    line.record_last_track,
    mask=([17, 18, 21], slice(None)),  # select particles 17,18,21 and all turns
    projections=False,
)

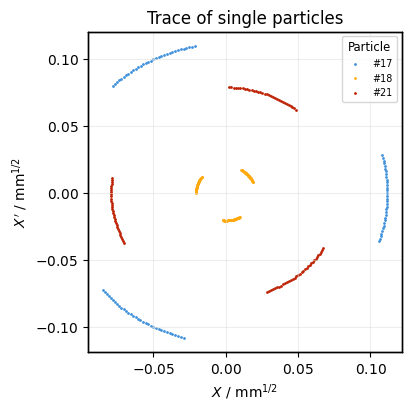
Plot the trace of some particles as distinct plots on the same axis:

ax = None
for particle_i in (17, 18, 21):
    plot = xplt.PhaseSpacePlot(
        line.record_last_track,
        mask=(particle_i, slice(None)),  # select particle i and all turns
        scatter_kwargs=dict(label=f"#{particle_i}"),
        kind="X",
        twiss=tw,
        titles=("Trace of single particles",),
        ax=ax,  # draw on same plot as before
    )
    ax = plot.ax

ax.legend(title="Particle");

---

See also

• xplt.phasespace