Timestructure (Spill, Schottky)

For some applications it is important to consider the particle arrival time, taking the longitudinal coordinate zeta into account. This includes non-circular lines, characterisation of extracted particle spills or long-term studies of coasting beams. The particle arrival time is:

\[\begin{equation*} t = \frac{\mathtt{at\_turn}}{f_\mathrm{rev}} - \frac{\mathtt{zeta}}{\beta_0 c_0} \end{equation*}\]

where the first term is only relevant for circular lines.

The plots in this guide are all based on the particle arrival time.

Show imports Hide code cell content

%load_ext autoreload
%autoreload 2

import xtrack as xt
import xpart as xp
import xplt
import numpy as np
import matplotlib as mpl
from matplotlib import pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import display, HTML

xplt.apply_style()

np.random.seed(43543557)

Show line generation code Hide code cell content

## Generate a simple 6-fold symmetric FODO lattice

n = 6  # number of sections
elements = {
    "QF": xt.Multipole(length=0.3, knl=[0, +0.63]),
    "QD": xt.Multipole(length=0.3, knl=[0, -0.48]),
    "MU": xt.Multipole(length=0.5, knl=[np.pi / n], hxl=[np.pi / n]),
}
parts = {
    "a": [
        xt.Node(0.7, "QF"),
        xt.Node(1.4, "MU"),
        xt.Node(2.1, "QD"),
        xt.Node(2.8, "MU"),
    ],
    "b": [
        xt.Node(2.2, "MU"),
        xt.Node(2.9, "QD"),
        xt.Node(3.6, "MU"),
        xt.Node(4.3, "QF"),
    ],
}
nodes = [xt.Node(5.0 * i, "a" if i % 2 else "b", name=f"S{i+1}") for i in range(n)]

# sextupoles
for i in range(n):
    sx = xt.Multipole(length=0.2, knl=[0, 0, 0.5 * np.sin(2 * np.pi * (i / n))])
    nodes.append(xt.Node(0.2, sx, from_=f"S{i+1}", name=f"S{i+1}SX"))

# aperture
nodes.append(xt.Node(0, xt.LimitRect(min_x=-0.01, max_x=0.01), name="APERTURE"))

line = xt.Line.from_sequence(
    nodes, length=5.0 * n, sequences=parts, elements=elements, auto_reorder=True
)
line.particle_ref = xp.Particles()
line.build_tracker();

Show particle generation code Hide code cell content

## Generate particles
nparticles = int(1e4)

# Transverse distribution (gaussian)
norm_emitt_x = 3e-6  # normalized 1-sigma emittance in m*rad (=beta*gamma*emitt_x)
norm_emitt_y = 4e-6  # normalized 1-sigma emittance in m*rad (=beta*gamma*emitt_y)
x, px = xp.generate_2D_gaussian(nparticles)
y, py = xp.generate_2D_gaussian(nparticles)

# Longitudinal distribution (coasting beam)
rel_momentum_spread = 1e-4  # relative momentum spread ( P/p0 - 1 )
zeta = line.get_length() * np.random.uniform(-0.5, 0.5, nparticles)
delta = rel_momentum_spread * xp.generate_2D_gaussian(nparticles)[0]

particles = line.build_particles(
    x_norm=x,
    px_norm=px,
    nemitt_x=norm_emitt_x,
    y_norm=y,
    py_norm=py,
    nemitt_y=norm_emitt_y,
    method="4d",  # for twiss (default is 6d, won't work without a cavity)
    zeta=zeta,
    delta=delta,
)


# generate a timeseries dataset of particle arrival times
counts = np.random.poisson(5, 10000) ** np.linspace(2, 1, 10000)

Show tracking code Hide code cell content

## Twiss
tw = line.twiss(method="4d")

## Track
line.track(particles, num_turns=500, turn_by_turn_monitor=True)

Scatter over time

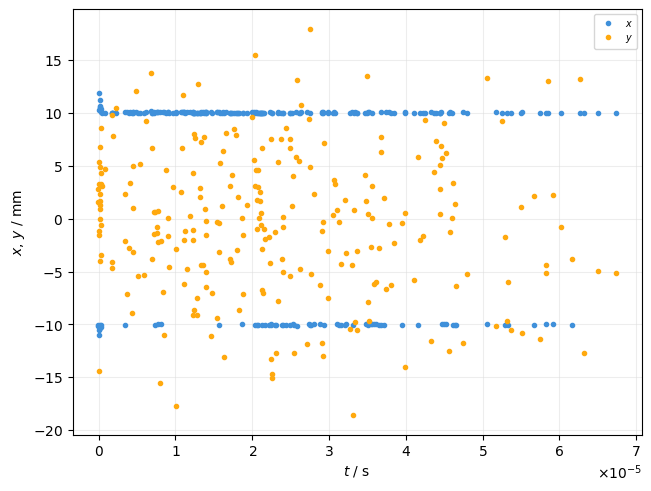
The TimePlot allows to plot any particle property as function of time. Here we plot x and y when the particles are lost.

plot = xplt.TimePlot(particles, "x+y", mask=particles.state <= 0, twiss=tw)

Binned time series

The TimeBinPlot allows to plot particle counts or averaged properties as time series with a given resolution.
Thereby all particles arriving within the interval defined by the time resolution are counted or averaged over.
The time resolution can be given with the bin_time keyword argument.

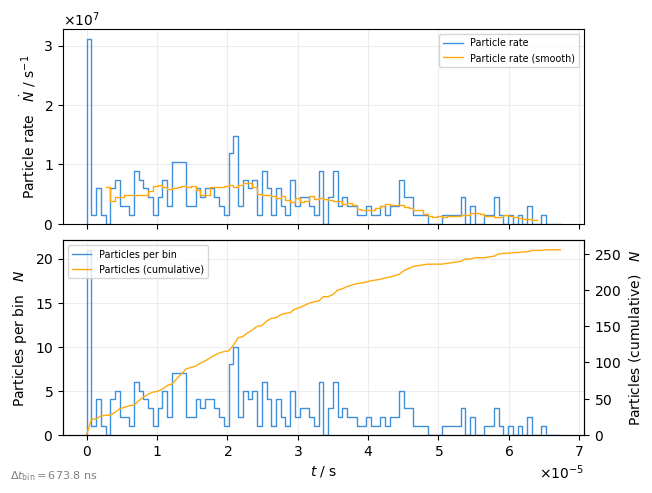
Spill intensity

Plot number of lost particles as function of time of slow extraction

plot = xplt.TimeBinPlot(
    particles,
    "rate+smooth(rate,n=10),count-cumulative",  # what to plot
    mask=particles.state <= 0,  # lost particles
    twiss=tw,
)

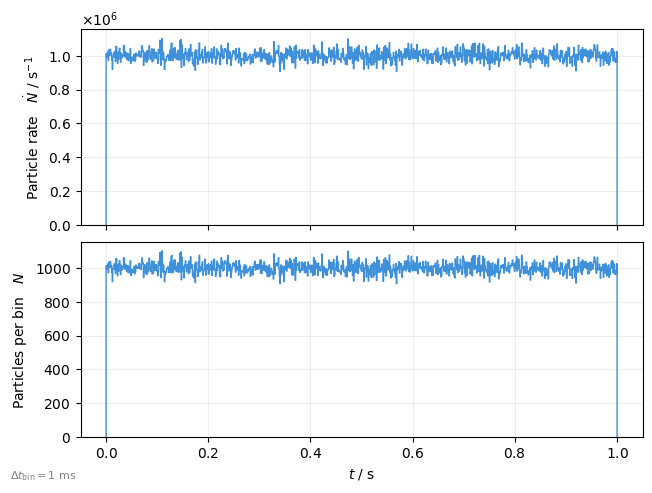
The TimeBinPlot and also many of the following plots supports passing an existing timeseries data instead of (timestamp based) particle data. This is useful to work with data from beam monitors or measurements.

binned_counts = xplt.Timeseries(np.random.poisson(100, size=10000), dt=1e-4)

plot = xplt.TimeBinPlot(
    # timeseries=binned_counts,  # this assumes the timeseries represents counts
    #                            # because 'kind=...' is count-based (rate=counts/s)
    timeseries=dict(count=binned_counts),  # Explicit is better than implicit
    kind="rate,count",
    bin_time=1e-3,
)

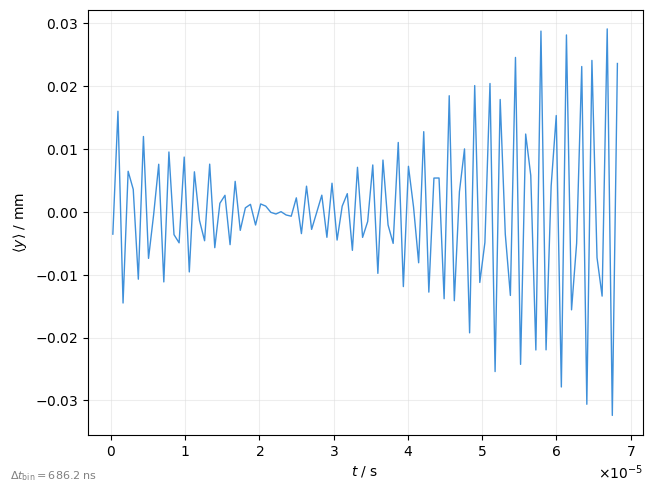
Transverse beam position (BPM)

Plot average y-position as function of time

plot = xplt.TimeBinPlot(
    line.record_last_track,
    "y",  # y-position
    # moment=1,  # the average (this is the default anyways)
    twiss=tw,
)

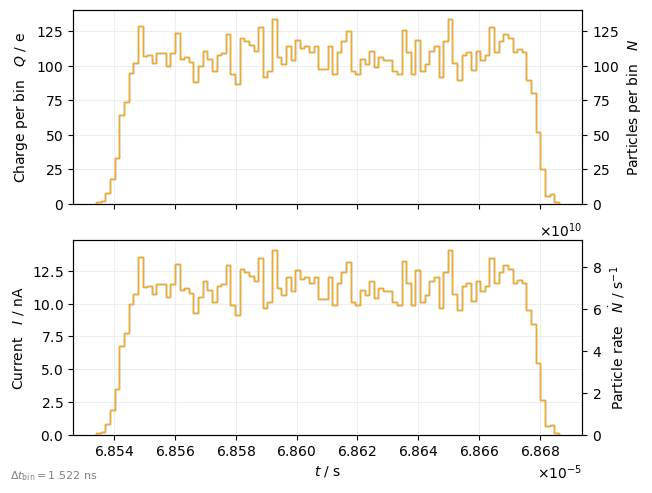
Longitudinal bunch shape

Plot charge as function of time

plot = xplt.TimeBinPlot(
    particles,
    "charge-count,current-rate",
    twiss=tw,
    mask=particles.state > 0,  # alive particles
)
plot.legend(show=False)

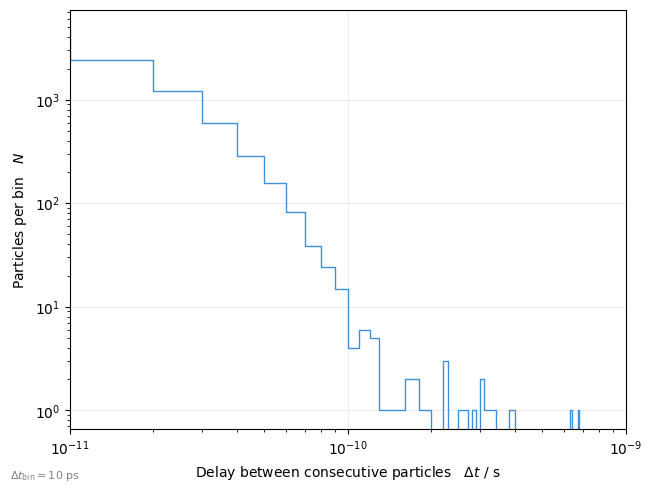
Consecutive particle delay

The TimeIntervalPlot allows analysis of the delay between consecutive particles.

plot = xplt.TimeIntervalPlot(particles, dt_max=1e-9, log=True, twiss=tw)

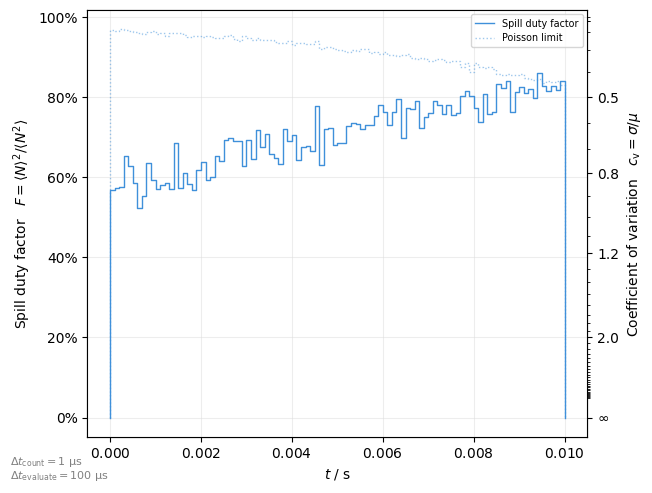
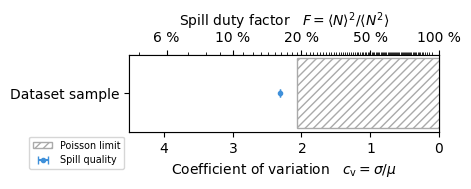
Spill quality

The following metrices exists to quantify the fluctuation of particle numbers in the respective bins:

• cv: Coefficient of variation

• duty: Spill duty factor

• maxmean: Maximum to mean ratio

These are useful to assess the spill quality.

Plot a metric as function of time in the spill

plot = xplt.SpillQualityPlot(
    # particles, mask=particles.state <= 0, twiss=tw, # pass the lost particles
    timeseries=xplt.Timeseries(  # we can also use pre-binned timeseries data instead
        counts, dt=1e-6
    ),
    kind="duty",
    counting_dt=None,  # interval for particle counting for (re-)binning
    evaluate_dt=None,  # interval to evaluate metric
)

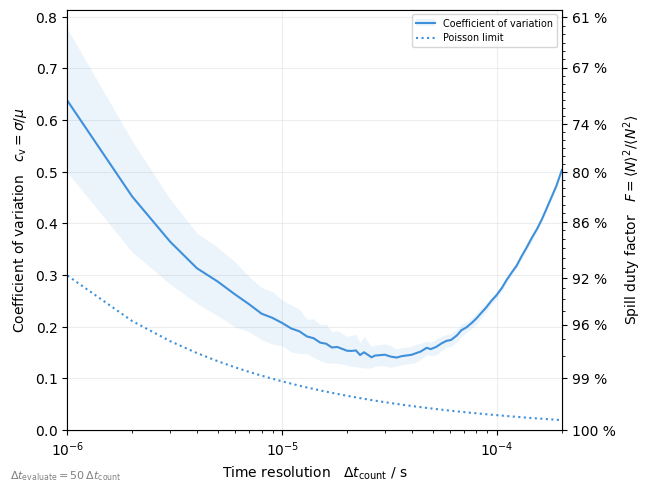
Plot a metric as function of timescale (counting bin time)

plot = xplt.SpillQualityTimescalePlot(
    # particles, mask=particles.state <= 0, twiss=tw, # pass the lost particles
    timeseries=xplt.Timeseries(
        counts, dt=1e-6
    ),  # or we can also use pre-binned timeseries data instead
    kind="cv",
)

Make a custom spill quality plot

dt_count = 50e-9
bins = 1000
dt_evaluate = dt_count * bins

# use helper to calculate metric
helper = xplt.TimeBinMetricHelper(twiss=tw)
t_min, dt_count, counts = helper.binned_timeseries(
    particles, dt_count, mask=particles.state <= 0
)
Cv, Cv_poisson = helper.calculate_metric(counts, "cv", bins)

# plot it
fig, ax = plt.subplots(figsize=(4, 1), constrained_layout=True)
style = dict(marker=".", ls="", capsize=3, label="Spill quality")
ax.errorbar(np.nanmean(Cv), ["Dataset sample"], xerr=np.nanstd(Cv), **style)
style = dict(hatch="////", ec="#aaa", fc="none", label="Poisson limit")
ax.add_patch(
    mpl.patches.Rectangle((np.nanmean(Cv_poisson), -0.15), -10, 0.3, **style)
)
ax.set(xlim=(4.5, 0))

# use helper to style axes
helper._link_cv_duty_axes(ax, ax.twiny(), True, "x")
ax.legend(loc="upper right", bbox_to_anchor=(0, 0));

Frequency domain

The TimeFFTPlot allows frequency analysis of particle data. Therefore the data is first binned into an equidistant time series as described above, and then an FFT is performed. This allows to plot the frequency spectrum of particle arrival time:

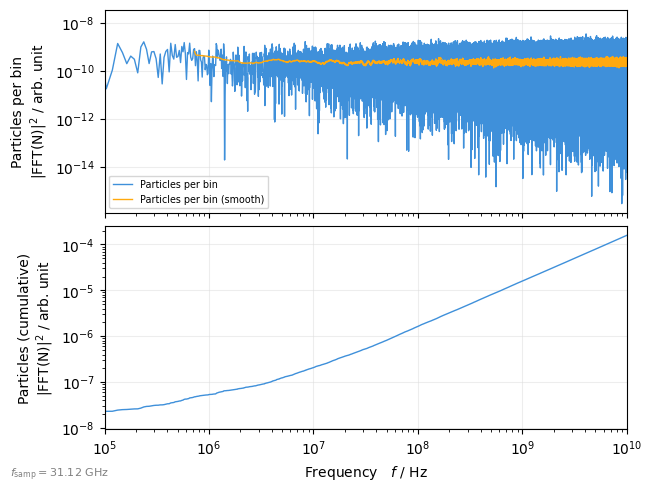
Spill fluctuations

plot = xplt.TimeFFTPlot(
    particles,
    "count+smooth(count,n=100),cumulative",
    mask=particles.state <= 0,  # only lost particles
    fmax=1e10,
    log=True,
    twiss=tw,
)
plot.ax[0].set(xlim=(1e5, None))
for a in plot.ax:
    a.set(ylabel=a.get_ylabel().replace("   ", "\n"))

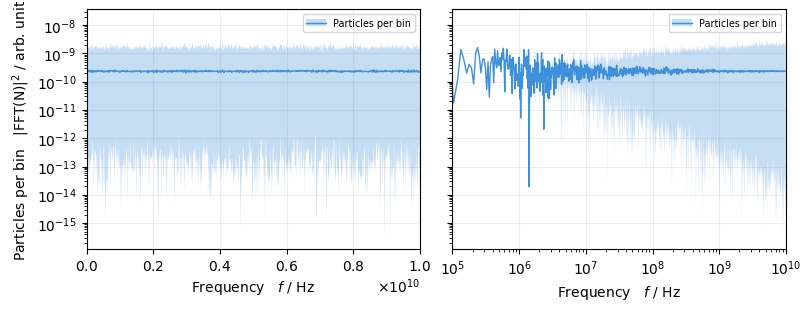
Since log-scaled FFT’s are typically very noisy, we can activate averaging. This does not only help to compare multiple FFTs in a single plot, it also reduces the number of datapoints to plot which speeds up rendering. The range (min/max) of the original data is shown as shodow to give an impression of how the FFT would look like without the averaging applied:

fig, ax = plt.subplots(1, 2, figsize=(8, 3), sharey=True)

for i, a in enumerate(ax):
    plot = xplt.TimeFFTPlot(
        particles,
        mask=particles.state <= 0,
        twiss=tw,
        fmax=1e10,
        log="xy" if i else "y",
        averaging=dict(
            lin=1000,  # for lin-scaled plots: integer number of bins to average
            log=1.01,  # for log-scaled plots: increment factor for bin number
        )["log" if i else "lin"],
        averaging_shadow_kwargs=dict(alpha=0.3),  # options to adjust the shadow
        ax=a,
    )
ax[1].set(xlim=(1e5, None), ylabel=None);

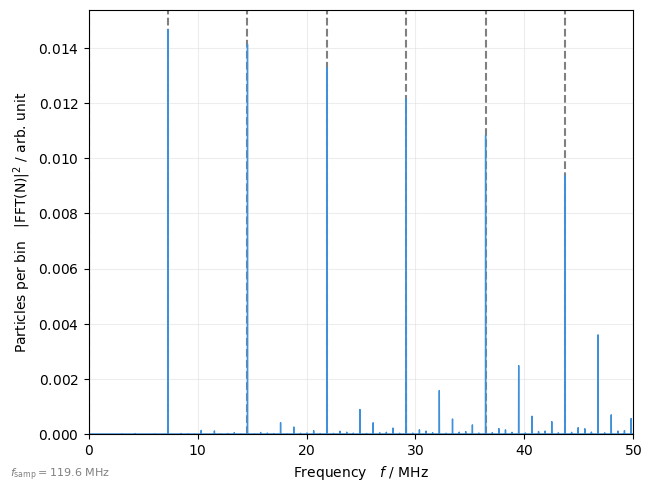
Longitudinal schottky spectrum

# select only a single particle
mask = (0, None)

plot = xplt.TimeFFTPlot(
    line.record_last_track,
    "count",
    mask=mask,
    fmax=50e6,
    log=False,
    display_units=dict(f="MHz"),
    twiss=tw,
)

frev = 1 / tw.T_rev0
for i in range(10):
    plot.ax.axvline(i * frev / 1e6, ls="--", color="gray", zorder=-1)

Tune or transverse schottky spectrum

Simmilary, the frequency spectrum of transverse motion (betatron tune spectrum) can be plotted. Note that the spectrum is based on transverse position as function of time and not as function of turn (this gives access to frequencies above half the revolution frequency and allows to avoid aliasing).

plot = xplt.TimeFFTPlot(
    line.record_last_track,
    "x-y",
    twiss=tw,
    relative=True,
    log=False,
    fmax=3 * frev,
    fsamp=30 * frev,  # high sampling frequency to reduce aliasing
)

for Q in (tw.qx, tw.qy):
    plot.ax.axvline(Q, ls="--", color="gray", zorder=-1)
    q, h = np.modf(Q)
    for h in range(int(plot.ax.get_xlim()[1] + 1)):
        [
            plot.ax.axvline(x, ls=":", color="lightgray", zorder=-1)
            for x in (h - q, h + q)
            if x != Q
        ]

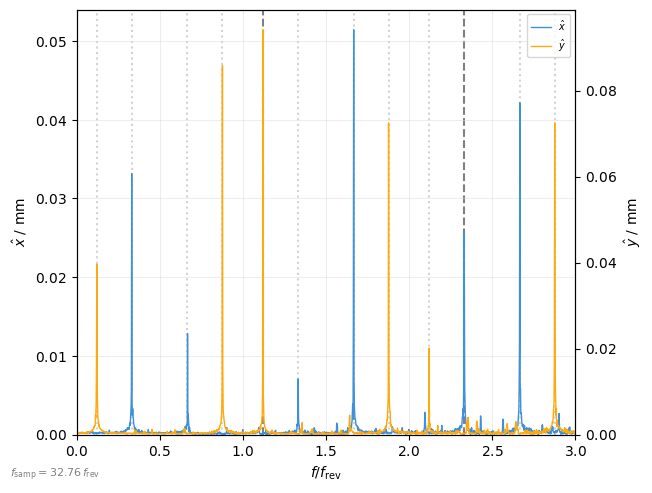
For reference, the spectrum of turn-by-turn positions:

Show code cell source Hide code cell source

from matplotlib import pyplot as plt

fig, ax = plt.subplots()
for xy in "xy":
    p = getattr(line.record_last_track, xy)[0, :]
    freq = np.fft.rfftfreq(len(p))
    mag = np.abs(np.fft.rfft(p))
    ax.plot(freq, mag, label=xy)
    ax.axvline(np.modf(getattr(tw, "q" + xy))[0], ls="--", color="gray", zorder=-1)
ax.legend()
ax.set(xlabel="$f/f_\\mathrm{rev}$", ylabel="FFT / a.u.", xlim=(0, 1), yscale="log");

---

See also

• xplt.timestructure